11. A New Method of Analysis
The Relational Method of Analysis
With Three Applications
Summary
After integrating the essential elements of logic, epistemology, linguistics, geometry, and mathematics into a functional unit called the relational method of analysis, the paper attempts to demonstrate that this new method can be consistently applied to a wide variety of disciplines in the physical as well as the moral sciences.
Abstract
This paper is an outcome of forty years of research in a variety of disciplines that contribute to a deeper understanding of economics. The ultimate result of this work is the beginning of a new system of thought that, for a large number of reasons, can appropriately be called relationalism. Relationalism is an expansion of rationalism. The aspiration of relationalism is to show that the unity of method of analysis leads to a unity of results that will gradually transform each individual science into an intellectual tool capable of solving correlated problems of intellectual and practical life.
Introduction
This paper is divided into three parts. The first part presents an outline of the relational method of analysis. The second part suggests how this method, consistently applied to a great variety of mental disciples, yields a new system of thought that for its internal integrity can be called relationalism. The third part suggests how this unified system of thought might help to solve concrete problems of daily living.
PART I — The Relational Method of Analysis
The relational method of analysis is composed of an integration of essential tools of the intellect that are scattered in five mental disciplines: logic, epistemology, linguistics, geometry, and mathematics. The very examination and creation of the new method of analysis has an immediate power of transformation upon these mental disciplines themselves. It infuses them with a new unified spirit and, to a small or large degree, leaves them qualitatively changed. Thus we obtain results that will eventually lead to relational logic, relational epistemology, relational linguistics, relational geometry, and relational mathematics. But, as we shall see, these fields do not represent five separate methodologies to be applied sequentially in any analysis. They are all applied at once. It is only during the exposition of the method itself that one separates its component elements from each other. The new method of analysis is a unitary entity.
This essential characteristic of relationalism can be briefly illuminated by reflection on what did our primordial ancestors do when they not only observed the moon and the salmon but, as Alexander Marshack (1) discovered, they actually recorded their observations; namely, when they put notations on bones upon bones that are still preserved in the world’s museums of art and anthropology. The sheer repetition of the single act of putting notations on bones compelled our ancestors to make use of three principles of logic: identity (this bone relates exclusively to facts about the moon) and non-contradiction (this bone does not relate to facts about the salmon) as well as equivalence (this scratch = a notation = knowledge about the moon, such as the shape of the moon tends toward roundedness, while the shape of the salmon remains oblong). These bones would have resulted into a meaningless heap, if our ancestors had not begun to use linguistics to distinguish among issues: if this object moves steadily and slowly across the horizon, we can call it moon; if this object moves erratically across the horizon, we can call it salmon. And in establishing these hypotheses were they not helped by geometry, namely the design of lines across the earth to indicate the horizon? And was not the analysis crowned by mathematics? They surely had to count how many times did the moon appear each year (twelve months!) across the horizon; and surely did they start measuring how many feet long was the distance between them and the horizon.
To repeat, our ancestors did not sequentially apply five separate methodologies in their analysis of the world. They applied them all at once. It is only during the exposition of the method itself that we need to separate those elements from each other.
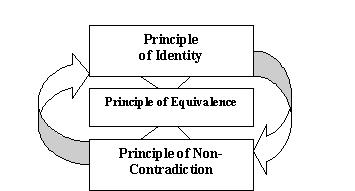
Toward Relational Logic
Relational logic results from the integration of three principles of logic: the principle of identity, the principle of non-contradiction, and the principle of equivalence into one unified system of analysis.
The principles of identity and the principle of non-contradictions are of such fundamental importance that—with the only exception of Hegel, as a consequence of his conception of the “inverted world” (2)—they have never been challenged in the history of the development of various systems of logic. Yet the third principle, the principle that links the two together, has changed constantly from classical logic to rational logic to dialectic logic and even eastern logic.
In classical logic, the third term was the principle of excluded middle: all things that are neither white nor black are excluded from the conversation, said Aristotle, and all Greek, Roman, and medieval philosophers. This solution lasted until the late Renaissance.
This approach was so evidently weak that it was replaced by Descartes with the principle of indifference. Allow me to be temporarily “indifferent” to gray, said Descartes (3); at the end of my analysis of (the number of) white and black pixels, you will know what gray is. This solution is still the governing rule of rational logic and—by extension—the governing rule of rationalism.
Two challenges to rational logic co-exist even today: one is Hegel’s dialectic logic, the other is Eastern logic. Dialectic logic accepts the principle of process, in which the thesis is transformed into the antithesis (hence the different function of the principle of non-contradiction) and then resolved into a synthesis. Eastern logic accepts the principle of transformation, whereby the Ying is transformed into the Yang, the night into the day, etc.
Dissatisfied with all these variations of the third principle of logic, during the 70’s this writer discovered that there is in logic—as well as in mathematics—a third principle. This is the principle of equivalence. Indeed, all textbooks on logic, as well as those on mathematics, contain detailed explanations of the principle of equivalence. And there the principle is left.
Relational logic is the beginning of a new system of logic that formally incorporates the principle of equivalence as the centerpiece of its very body. By putting this principle between the principle of identity and the principle of non-contradiction, one develops a powerful set of tools of analysis that, as we shall see, can be used systematically both to deconstruct mainstream theories and to develop on those foundations what can be properly called relational and/or Concordian theories.
Relational logic can be diagrammed as follows:
Figure 1. Relational Logic
Disregarding all details of the case, details that are firmly established in the textbooks on logic and mathematics, the relation among these three principles can be synthetically expressed in this fashion. Each one of these principles is essential to the analysis. Each one performs the same basic functions, but only strict adherence to all three principles together gives assurance that one is on solid logical ground.
The reader will have noticed that the three principles were consistently applied by our ancestral ancestors much before our thought process began to be codified by the Greeks.
Toward Relational Epistemology
The subject of epistemology is the understanding of reality and the establishment of truth. Through a gross simplification it can be said that, while most epistemology up to Descartes was composed of a set of ideas deduced through the complex rules of the syllogism, most epistemology since Descartes takes its lead from the fundamental proposition that facts are given to us by the senses and we study them and define them empirically—namely through a system of hypotheses and tests—via induction.
Within the scope of this paper, relational epistemology is not so much concerned with theoretical issues as with concrete tools of analysis. Thus—whether for inductive or deductive purposes—it accepts and makes use of the following tools of analysis: facts, names, ideas, concepts, theories, and systems of thought. These tools are well known and much used. The key contribution of relational epistemology is to consider these tools, not simply as a necessary progression, but especially as containers of a progressively larger amount of information. In relational epistemology, these tools are called synthesizers of information. The assumption, of course, is that they lead to a progressively more precise and larger understanding of reality and truth.
A more specific contribution made by relational epistemology is the clear-cut separation of the idea from the concept. Even Kant, who provided the most comprehensive specification of the concept (4), used the two terms interchangeably. But through an in-depth study of economics pursued over many years, it became clear to this writer that while ideas are allowed to contain contradictory reality—the idea of saving in mainstream economics, for instance, relates to wealth that is productive as well as nonproductive of further wealth—, the concept does not tolerate such internal contradictions. Hence, in Concordian economics (5, 6) one distinguishes between investment that relates only to productive wealth and hoarding that relates only to nonproductive wealth.
In order to establish the degree of reality and truth that each one of these tools contains, relational epistemology observes each fact, name, idea, concept, theory, and system of thought, not only in themselves, but as they relate to each other. Consequently, relational epistemology also adds the specific insight that facts are the determinates, not the determinants of the system. As Kuhn pointed out (7), the fact of “ether” disappears in modern physics; the fact of two parallel lines not meeting is denied in imaginary geometry. This seems to be a fair beginning of a comprehensive epistemology.
Toward Relational Linguistics
The rules of logic and epistemology are abstract rules that apply to any reasoning. For the discourse to become concrete, one has to realize not only that those rules apply to words, but that those rules are themselves made of words. Single words.
While single words are the beginning, they are not the end of wisdom. Hence relational linguistics incorporates the ancient study of grammar as the set of rules of how words relate to each other.
Men and women soon realized that words do not travel in couples either, one next to the other. Words are used in logical strings; hence men and women developed another mental discipline: the study of syntax. That is the study of propositions and it is an integral part of relational linguistics, because it is through propositions that one defines names, ideas, concepts, theories, and systems of thought.
One could make the mistake of reopening at this stage the discussion on epistemology. Better wisdom is to go forward. One then meets a third essential mental discipline: the study of rhetoric. This is the study of how to construct elegant and convincing sentences, and it is the third essential element of relational linguistics.
The central concern in our context is not beauty but truth. Hence we will stop here. After emphasizing that the study of linguistics has eventually to be seen—not as a linear sequential study—but as the steady integration of grammar, syntax, and rhetoric, we will move on to the application of geometry and mathematics as indispensable tools in the analysis of the truth of propositions—namely, the definition of names, ideas, concepts, theories, and systems of thought. Needless to say, we formulate theories and systems of thought not so much through geometry and mathematics as through linguistics. To say the least, it is linguistics that holds together even the most technical theories of mathematics and geometry.
Were one to abandon the field of linguistics at this point, one would reveal to be under the spell of The Great Rationalist Illusion: So caught up with the affairs of the mind, the cogito ergo sum of its birth, rationalism has made a skeletal analysis of many things, and it has neglected man. Thus it has fallen into the trap set up by Nietzsche, the force of the farce—which, were it purely an esthetic game, might even be enjoyable. Yet, the Nietzsche trap is an exaltation of the farce of force. Its children are Fascism, Nazism, and Communism.
Yes, words have meaning. Therefore, words have consequences. Let us spend a moment to get out of The Great Rationalist Illusion by looking at the mechanics of meaning and the mechanics of communication. That, after all, is the soul of linguistics—when linguistics is put in relation to concrete men and women.
The mechanics of meaning. The Great Rationalist Illusion assumes that words are indestructible nuggets of eternal truth. If men and women were angels, that might be the case. But men and women are neither angels nor disemboweled minds. As, for instance, Vitz stresses (8), they are the result of a spiritual integration of minds in a body, all wrapped up in a bundle of feelings. Hence the meaning of words changes constantly. Words are little gods—readers who might prefer the expression “words are torches or flash lights” are free to use this metaphor. Words are little gods that illuminate the meaning of reality. And yet, being uttered by limited human beings, words are at the same time little devils that hide the meaning of reality. As philosophers say, every affirmation is a negation. Hence, while the rules of logic and the rules of epistemology given above are essential to keeping the traffic of meaning honest, to understand the mechanics of meaning this now familiar diagram might help:
Figure 2. Mechanics of Meaning
It is enough to know that the meaning of colors is so completely different from culture to culture, to realize that, without keeping in mind that the meaning of what is said might be completely different when it is related to the speaker or the listener, communication easily results in miscommunication. The “what” is said, in other words, needs to be explicated and agreed upon by the speaker and the listener.
We will do that in the next part of this paper, the part that applies the new method of analysis to a variety of mental disciplines.
The mechanics of communication. For the time being, lets us be aware of the other function of linguistics, a function that can be called the mechanics of communication. In every communication, there is the How, the What, and the Who. Their relationship can again be better visualized if it is put in the familiar diagrammatic form:
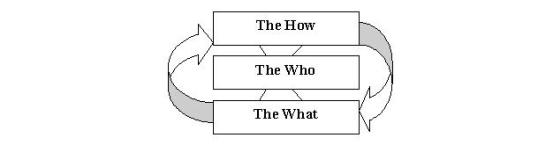Figure 3. Mechanics of Communication
The method of analysis we are explicating is the How, the What is the topic of the next part of this paper. The Who is the full bodied man and woman composed of mind, body, and heart. In the search for meaning and truth, the study of linguistics is basic; but, as Professor Paul A. Samuelson never tires of repeating, mathematics and geometry help.
Toward Relational Geometry
Geometry, including fractal geometry, is not only a set of essential tools of analysis that help us reveal truths that otherwise might remain hidden. It is also a set of tools that help us visualize the reality. Thus these tools are safe guides to our imagination as well as our intellect.
There are many ways in which the new method of analysis calls upon geometry in the course of its investigations. Specific ways are detailed during the solution of specific problems. Here we will remain at a much higher level of generality. We will outline only three mental processes through which a line is transformed into a sphere. This is the essence of this paper, after all: We are transforming the linear method of analysis of rationalism into the organic and dynamic method of analysis of relationalism. We are expanding the rational into a relational method of analysis.
First, let us go back to Figure 1. Let us dismantle that figure, and take one rectangle at a time. Let us shrink the rectangle to the smallest possible size. Have we not obtained a segment of a line? This is the reverse of the process outlined by Mandelbrot (9), who explains: “The limit Peano curve establishes a continuous correspondence between the straight line and the plane.”
But one line is a very reductionist approach. Surely there is more than one thing that we want to analyze at once. By repeating the procedure for the other two rectangles, we obtain at least three lines. Indeed, if we multiply the number of lines, and we let them all pass through one single focal point, otherwise the analysis goes haywire, we obtain the following figure:
Figure 4. Intersecting Segments
Rotating this figure about its center at ever increasing speed, we obtain the image of a circle. And what is a circle if not the two-dimensional image of a sphere? We have thus transformed the line into a sphere. (One can build a sphere from a circle with this approach. Take the circle by its center, then reach for the shadow point of the center—namely, the “back” of the center point. Gradually extend the two points to the same distance as the diameter of the circle. The result is a sphere. This operation establishes an equivalence relation among the point, the circle, and the sphere. Mandelbrot would say that the three concepts differ in scale, but are self-similar in structure.)
Let us go back again to Figure 1, and follow a different approach. Let us take only one rectangle and spin the rectangle at ever increasing speed around its geometric center. Do we not see a circle? And what is a circle if not a two-dimensional image of a sphere?
Third approach. Let us go back again to Figure 1 and rotate the entire figure at ever increasing speed around its geometric center. Again, do we not see a circle? And what is a circle if not a two-dimensional image of a sphere? Indeed, at this point, we are entitled to identify an even more complex picture. To do that, we need to superimpose the three rectangles upon each other and then rotate them at once. Do we not obtain the image of three intercompenetrating spheres rotating synchronously into each other?
In a sphere, all lines relate to each other in many complex ways. With the help of geometry, we have not only transformed a line into a sphere. We are also transforming the rational method of analysis, the study of individual lines, into a relational method of analysis, the study of many interrelated lines at once.
Toward Relational Mathematics
Much of mathematics—and the measurement of geometric figures—is built upon equivalence relations. A triangle is a set of equivalence relations; trigonometry is built on an equivalence relation; the relation between three fingers (digits, or items in the decimal system), the symbol “three”, and three apples is an equivalence relation; the First Outer, Inner Last (FOIL) relation between two fractions expresses on an equivalence relation; a system of equations is built on an equivalence relation—just as the syllogism of old was.
The most fundamental equivalence relation that is of interest at this point is this:
0 = 1 = ∞,
which reads: zero is equivalent to one and one is equivalent to infinity.
This expression makes sense as soon as one realizes that 0, 1, and infinity are whole systems in themselves—observed from three different points of view. The meaning of this equivalence will become clearer as we proceed to the substance of the arguments. For the time being, it might be worth to observe that two thirds of the content of mathematics does not lend itself to measurement. The concept of zero and the concept of infinity are not measurable entities. They are kept at bay by the very practical device of the limit. The number system approaches, but never reaches, either zero or infinity.
PART II — Three Applications
In this part we will try to see how the consistent use of the method outlined above leads to new insights into three well-established, ancient mental disciplines: biology, economics, and physics. These insights are of such fundamental importance that they transform the disciplines themselves. And, since these insights are not only related within each discipline but they even establish relations across disciplines, it can safely be said that when the analysis is extended to many other disciplines, and an entire new body of knowledge is developed, this corpus can properly be called relationalism. Let us start with biology.
Toward Relational Biology
Looking at it from the outside, one definitely assumes that biology is a science—with all that such an attribute entails. The field is assumed to be full of certainties and self-assurance. But that is the view from the outside. The view from inside is completely different. Succumbing to the shortcomings of the rational method of analyzing one species at a time, biology is not being of much help in a field with which this writer has been intimately connected for the last forty years: fisheries development (10). In the United States, the science has been politicized in the implementation of its recommendations through the Regional Fisheries Management Councils. In other words, rather than order and equilibrium, havoc reigns—accused of being engaged in overfishing and subject to draconian regulations concerned with the depletion of traditional bottom fish species, fishermen are loosing their means of livelihood, while economic infrastructures built over the centuries are being dismantled, and communities are dissolved.
The solution must start at the level of science. The field of study must be enlarged to correspond with the reality of the field it encompasses. In other words, from the species to species approach to the study—and management—of fish, one must pass to the comprehensive predator-prey model of the biomass as a whole. The model is as follows:
Figure 5. Predator-Prey Model
This model, which started as the Lotka-Volterra model in the 1920’s (11), is being used to analyze a variety of biological relationships concerning the wolves, the deer, even the lemmings, as reported in Science on 4 November 2003—and their predators. For the New England fisheries, this model suggests that one cannot manage bottom fish species one at a time. It is necessary to expand one’s field of vision to encompass the pelagics as well, those fish that live in the midwater column and intercept the larvae of the bottom fish—such as cod and haddock—when they go up to the surface of the ocean toward food and light as well as when the codlings try to go back to their habitat at the bottom of the ocean. Clearly, when they go up and down the water column, bottom fish become a feast for the pelagics, mostly herring and mackerel, species that at present are in extremely abundant supply. Overfishing there is. Yet, overfishing is done, not by the fishermen, but by the predators of such traditional species as cod and haddock and flounder.
These relationships have been quantified in a massive study, available at http://gloucestercdc.org/GCDC_Tools.html, thanks to volunteer assistance from Dr. Peter Otto, Jeroen Struben, and Sanghyun Lee, three members of the System Dynamics graduate program at MIT, under the direction of Professor Jim Hines. The concern here is neither with the numbers, or the refinements of the model, nor with the implications of the numbers in relation to fisheries management issues. The concern is with the transformation of biology from a linear to a relational discipline—as part of the application of the new method of analysis to a variety of mental disciplines.
The Transformation of Mainstream Economics
These days, to set aright the daily life of a coastal community such as Gloucester, Massachusetts, the development of a comprehensive science of biology needs to be fully integrated into the study of economics (12). And yet, as soon as one engages in this enterprise one realizes that mainstream economics—suffering from a premature application of mathematics to economics (13)—is not concerned with stocks of real wealth, but is almost exclusively concerned with flows of monetary values. Thus, one encounters the dichotomy of Wall Street vs. Main Street. Clearly, mainstream economics must be transformed to serve the realities of daily life (14).
The seed of the transformation of mainstream economics was planted in 1965 when this writer changed the second equation of Keynes’ (15) model of the economic system from Saving = Income – Consumption to Investment = Income – Saving (or, better, Hoarding).
Indeed, mathematics dictated the transformation of the entire model from
Income = Investment + Consumption
Saving = Income – Consumption
Saving = Investment
TO
Income = Hoarding + Consumption
Investment = Income – Hoarding
Investment = Consumption.
Toward Concordian Economics
Having produced two equally consistent models, mathematics could go no further. It was of no assistance in choosing between the two models; it was temporarily neutralized as a tool of analysis. It was then that this writer recurred to logic and epistemology. And it was there that he found the tools to analyze the two systems: these are the tools that are gradually being systematized into the relational method of analysis outlined above. Eventually, the pivotal step turned out to be the need (16) to transform the Investment = Consumption equation into the following equivalence:
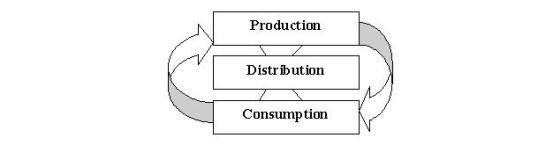
Investment = Distribution = Consumption.
Leaving all technical details aside, once the word Investment was transformed back into the word of classical economics, Production, it became possible to formulate the following diagram, and this figure in turn helped visualize the economic process.
Figure 6. The Economic Process
What is important to realize in this context is that economics was thus transformed from a linear to a relational discipline. As can be seen form this figure, the lines of supply and demand are all put in relation with each other (the supply of all production has to be demanded by consumers; and consumers have to have the means to purchase that production: money must already have been distributed among them). Indeed, one of the reasons this new framework of analysis is called Concordian economics is that, mutatis mutandis, it brings into relational concord three major schools of current economic thought: supply-side economics, institutional economics, and demand-side economics. Another reason for this name is that this model applies to both macro and microeconomics. The model represents the economy of the individual person as well as the economy of a firm, a city, a nation or, even, the world as a whole.
On the basis of this model, it is possible to build an economic policy that is just and can be implemented through a set of economic rights and responsibilities (17-19).
With Concordian economics, the seed of relationalism had blossomed into a full flower. And the mental process did not stop there. Apart from further developments in economics, here is the next major extension, which attempted to answer the key related question: Are there enough natural resources to implement a just economic policy?
From Physics to Metaphysics
The easiest application of relational tools of analysis occurred to this writer at about thirty thousand feet in the air, in a field he knew almost nothing more than a few generalities. This is physics. And yet the discovery is of fundamental importance. As we all know, Einstein wrote E = mc2. What is less known is that he defined this relationship as an equivalence (20). Where is the third term, this writer inquired? And of course, at thirty thousand feet in the air, the answer comes in an easy way. The third term is spirit. It became thus possible to establish this equivalence: matter = energy = spirit. And once down on earth, this relation was eventually diagrammed in the usual fashion:
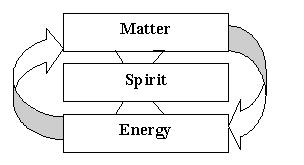
Figure 7. The Relational Reality
Figure 7 can be read, not only to mean that matter transforms itself into energy and energy into matter, but especially along these lines. The world in which we live has to be observed first from the point of view of matter and then from the point of view of energy. The essential prerequisite is to see these two aspects of reality not in linear fashion, but in a relational fashion, namely as two separate and distinct points of view. And when that is done, one can easily see that the total reality in which our daily existence is immersed can be grasped only if it is also observed from a third point of view: the viewpoint of the spirit.
The conclusion that is of immediate concern is this. If spirit is infinite, then it is very likely that both matter and energy are also infinite. Resources are of course finite at any specific moment in time and place, but they are potentially infinite—and the history of mankind confirms that much. There is no scarcity in the world of natural resources.
The conclusion that is of more long term interest is this. We have thus come back to the very roots of our civilization. Our ancestral ancestors—and many brothers and sisters in many other civilizations of today—started their analysis neither from matter nor, certainly, from energy. They started the analysis form the point of view of spirit. With the equivalence of matter to energy and to spirit, we have a chance of starting everything all over again (21).
PART III — Toward Concord in Intellectual Affairs
What is the promise of relationalism? The fundamental promise is that unity of method of analysis will unavoidably lead to unity of action in fighting age-old scourges of mankind. To make the universal local, if relational biology is analyzed in depth as it applies to Gloucester, if it is incorporated into Concordian economics, and if physics assures us that we do not live in a world of scarcity, we might be able to break the back of some of the oldest curses of mankind. If people are granted the opportunity to create all the wealth that they need, poverty will be abated, greed will be held in check (it costs personal effort to create wealth), and our intellectuals, rather than fighting for supremacy of their ideas, might work for the common good—the betterment of our precious little community.
Conclusion
Does relationalism stand any chance against the powerful traditions of rationalism? The answer has to be positive. First of all, relationalism stands on the very shoulders of rationalism. There is no long-term antagonism there. And then, it seems that there is much room for common cause with the many stirrings that are evident today in each and every discipline.
Footnotes
1. A. Marshack, The Roots of Civilization: The Cognitive Beginnings of Man’s First Art, Symbol, and Notation (McGraw Hill, New York, 1972).
2. H-G. Gadamer, Hegel’s Dialectic: Five Hermeneutical Studies, P. C. Smith Trans. (Yale Univ. Press, New Haven and London, 1976), pp. 35-53.
3. R. Descartes, Discourse on the Method of rightly conducting the reason and seeking the truth in the sciences (Collier, New York, [1637] 1938), p. 60.
4. I. Kant, Critique of Pure Reason, F. M. Muller Trans. (Doubleday, Garden City, N.Y., 1966), pp. 66-67.
5. Anon. (2002). “The Economic Process: An Instantaneous Non-Newtonian Picture. By Carmine Gorga” (Annotated Listing of New Books). J. Econ. Lit. 40, 1306 (2002).
6. P. Davidson, “The Economic Process: An Instantaneous Non-Newtonian Picture. By Carmine Gorga” (A Book Review). J. Econ. Lit. 41, 1284 (2003).
7. T. S. Kuhn, The Structure of Scientific Revolution (Univ. of Chicago Press, Chicago, 1962).
8. P. C. Vitz, “The Crisis in the Psychological Concept of Self or Person: A Neo-Thomist and Personalist Answer,” Catholic Social Scence. Rev. 8, 63 (2003).
9. B. B. Mandelbrot, The Fractal Geometry of Nature (New York, W. H. Freeman, 1983), p. 62.
10. C. Gorga, L. J. Ronsivalli, Quality Assurance of Seafood (Van Nostrand Reinhold, New York, 1988).
11. R. H. Abraham, C. D. Shaw, Dynamics—The Geometry of Behavior. Part 1: Periodic Behavior (Aerial Press, Santa Cruz, CA, 1981), pp. 83-86.
12. C. Gorga, S. B. Weeks, “Fisheries Renewal: A Renewal of the Soul of Business,” Catholic Social Sci. Rev. 2, 145 (1997).
13. J. M. Keynes, “Professor Tinbergen’s Method,” Econ. J. 49, 558 (1939).
14. C. Gorga, The Economic Process: An Instantaneous Non-Newtonian Picture (Univ. Press of America, Lanham, Md., and Oxford, 2002).
15. J. M. Keynes, The General Theory of Employment, Interest, and Money (Harcourt, New York, 1936), p. 63.
16. R. G. D. Allen, Mathematical Economics (Macmillan and St. Martin’s, London and New York, ed. 2, 1970), p. 748.
17. C. Gorga, “Bold New Directions in Politics and Economics,” Human Economy Newsletter, 12, 3 (1991).
18. _____ “Four Economic Rights: Social Renewal Through Economic Justice for All,” Social Justice Rev. 85, 3 (1994).
19. _____”Toward the Definition of Economic Rights,” J. of Markets and Morality 2, 88 (1999).
20. F. Capra, The Tao of Physics (Random House, New York, 1975).
21. As quoted in O. Nathan, H. Norden, eds. Einstein on Peace (Avnet Books, New York, 1981 ed, p. 376), from a pamphlet published by Beyond War in 1985 entitled A New Way of Thinking, in 1946, Albert Einstein said: “The unleashed power of the atom has changed everything save our modes of thinking.” If the proposed method of analysis is accepted, and matter is seen as equivalent to energy and energy equivalent to spirit, then everything changes.
The writer wishes to acknowledge the enormous assistance in the development of this system of thought received over many years from Professor Franco Modigliani, a Nobel laureate in economics at MIT, and M. L. Burstein, a professor of economics at York University. Mark Perlman, Charles T. Wood, Buckminster Fuller, Alan Reynolds, Michael J. Naughton, Rudy Oswald, Robert F. Drinan, John J. Neuhauser, Michele Boldrin, William J. Baumol, and Howard Zinn have expressed especially strong support for various parts of my work. To all thanks.
Relationalism 
